Skip to article frontmatterSkip to article content

4.10

考虑第4.8.1节中描述的另一种误差函数：

E(w→)≡12∑d∈D∑k∈outputs(tkd−okd)2+γ∑i,jwji2E(\overrightarrow{w}) \equiv \frac{1}{2} \sum_{d \in D} \sum_{k \in outputs} (t_{kd} - o_{kd})^2 + \gamma \sum_{i, j} w_{ji}^2
(1)

为这个误差函数E推导出梯度下降更新法则。证明这个权值更新法则的实现可通过在进行表4-2的标准梯度下降权更新前把每个权值乘以一个常数。

先看一下表4-2的标准梯度下降权重更新法则：

表4-2 包含两层 sigmoid 单元的前馈网络的反向传播算法（随机梯度下降版本）

BACKPROPOGATION(training_examples,η,nin,nout,nhidden)traning_examples中每一个训练样例是形式为<x→,t→>的序偶，其中x→是网络输入值向量，t→是目标输出值。η是学习速率（例如0.05）。nin是网络输入的数量，nhidden是隐藏层单元数，nout是输出单元数。从单元i到单元j的输入表示为xji，单元i到单元j的权值表示为wji。⋅创建具有nin个输入，nhidden个隐藏单元，nout个输出单元的网络⋅初始化所有的网络权值为小的随机值（例如−0.05和0.05之间的数）⋅在遇到终止条件前：⋅对于训练样例traning_examples中的每个<x→,t→>：把输入沿网络前向传播1.把实例x→输入网络，并计算网络中每个单元u的输出ou使误差沿网络反向传播2.对于网络的每个输出单元k，计算它的误差项δkδk←ok(1−ok)(tk−ok)3.对于网络的每个隐藏单元h，计算它的误差项δhδh←oh(1−oh)∑k∈outputswkhδk4.更新每个网络权值wjiwji←wji+Δwji其中Δwji=ηδjxjiBACKPROPOGATION(training\_examples, \eta, n_{in}, n_{out}, n_{hidden}) \\ traning\_examples 中每一个训练样例是形式为<\overrightarrow x, \overrightarrow t>的序偶，其中 \overrightarrow x 是网络输入值向量，\overrightarrow t 是目标输出值。\\ \eta 是学习速率（例如0.05）。n_{in}是网络输入的数量，n_{hidden} 是隐藏层单元数，n_{out} 是输出单元数。\\ 从单元i到单元j的输入表示为x_{ji}，单元i到单元j的权值表示为w_{ji}。\\ \cdot 创建具有n_{in}个输入，n_{hidden}个隐藏单元，n_{out}个输出单元的网络\\ \cdot 初始化所有的网络权值为小的随机值（例如-0.05和0.05之间的数） \cdot 在遇到终止条件前：\\ \cdot 对于训练样例 traning\_examples 中的每个<\overrightarrow x, \overrightarrow t>： \\ 把输入沿网络前向传播 \\ 1. 把实例\overrightarrow x输入网络，并计算网络中每个单元u的输出o_u\\ 使误差沿网络反向传播 \\ 2. 对于网络的每个输出单元k，计算它的误差项\delta_k \\ \delta_k \leftarrow o_k(1-o_k)(t_k - o_k) \\ 3. 对于网络的每个隐藏单元h，计算它的误差项\delta_h \\ \delta_h \leftarrow o_h(1-o_h)\sum_{k \in outputs} w_{kh}\delta_k \\ 4. 更新每个网络权值 w_{ji} \\ w_{ji} \leftarrow w_{ji} + \Delta w_{ji} \\ 其中 \\ \Delta w_{ji} = \eta \delta_j x_{ji}
(2)

对于一个8x3x8的网络，详细图形如下：

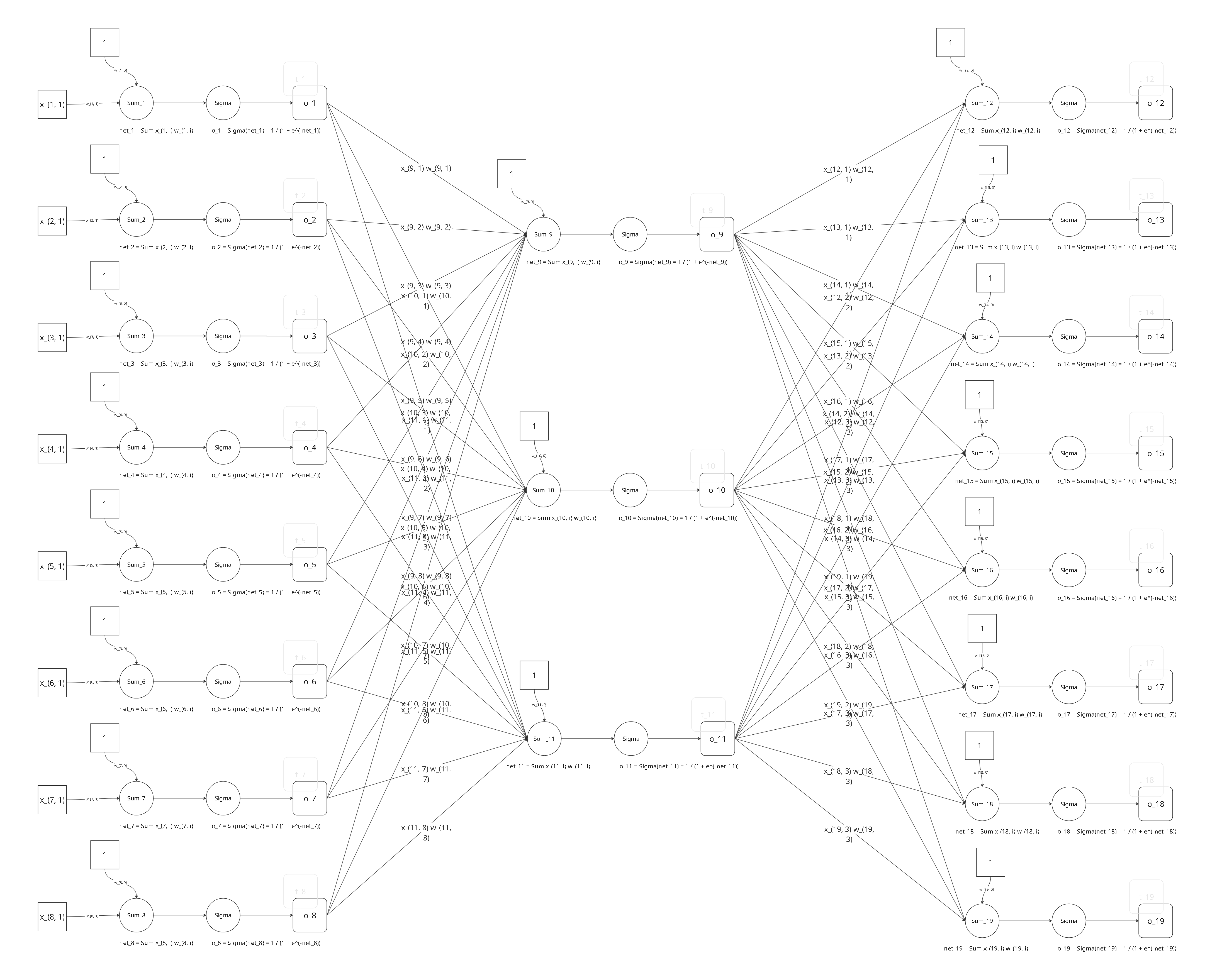
alt text

先来引入几个记号，以便于后面的推导。

令 Ed(w→)E_d(\overrightarrow{w}) 表示在训练样例 dd 上的误差函数：Ed(w→)≡12∑k∈outputs(tkd−okd)2E_d(\overrightarrow{w}) \equiv \frac{1}{2} \sum_{k \in outputs} (t_{kd} - o_{kd})^2。那么，在4.8.1节中描述的误差函数E可以写成：

E(w→)≡∑d∈DEd(w→)+γ∑i,jwji2E(\overrightarrow{w}) \equiv \sum_{d \in D} E_d(\overrightarrow{w}) + \gamma \sum_{i, j} w_{ji}^2
(3)

随机的梯度下降算法迭代处理训练样例，每次处理一个。对于每个训练样例d，本题要求利用整体误差 EE 的梯度来修改权值。换句话说，对于每一个训练样例d，每个权 wjiw_{ji} 被增加 Δwji\Delta w_{ji}：

Δwji=−η∂E∂wji\Delta w_{ji} = - \eta \frac{\partial E}{\partial w_{ji}}
(4)

我们的目标是求出∂E∂wji\frac{\partial E}{\partial w_{ji}}的一个表达式，以便实现随机梯度下降法则。可以看出，

∂E∂wji=∑d∈D∂Ed∂wji+2γwji\frac{\partial E}{\partial w_{ji}} = \sum_{d \in D} \frac{\partial E_d}{\partial w_{ji}} + 2\gamma w_{ji}
(5)

我们剩下的任务就是为∂Ed∂wji\frac{\partial E_d}{\partial w_{ji}}推导出一个方便的表达式。首先，注意权值 wjiw_{ji} 仅能通过 netjnet_j 影响网络的其他部分。

对于一个网络，其表示如下：

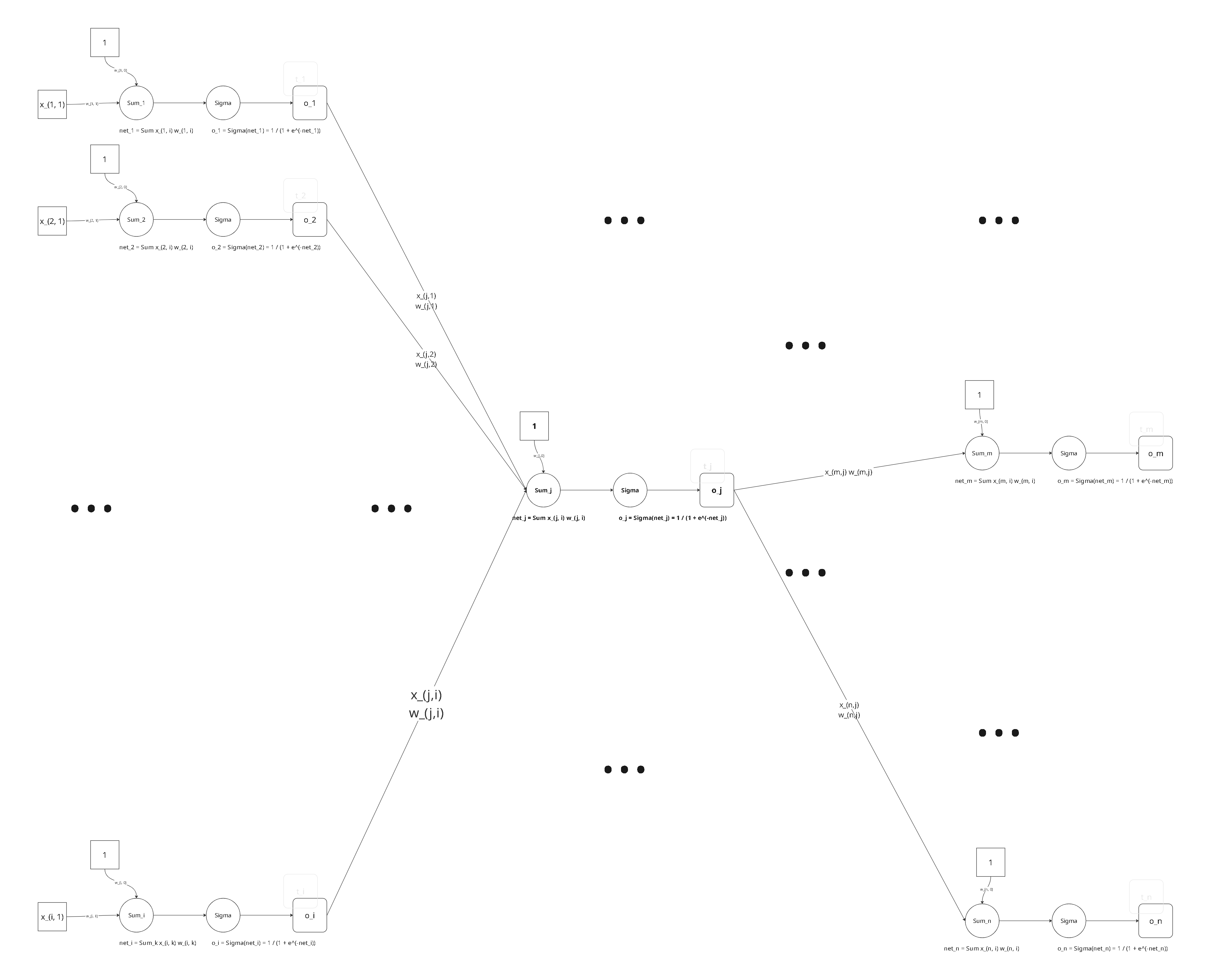
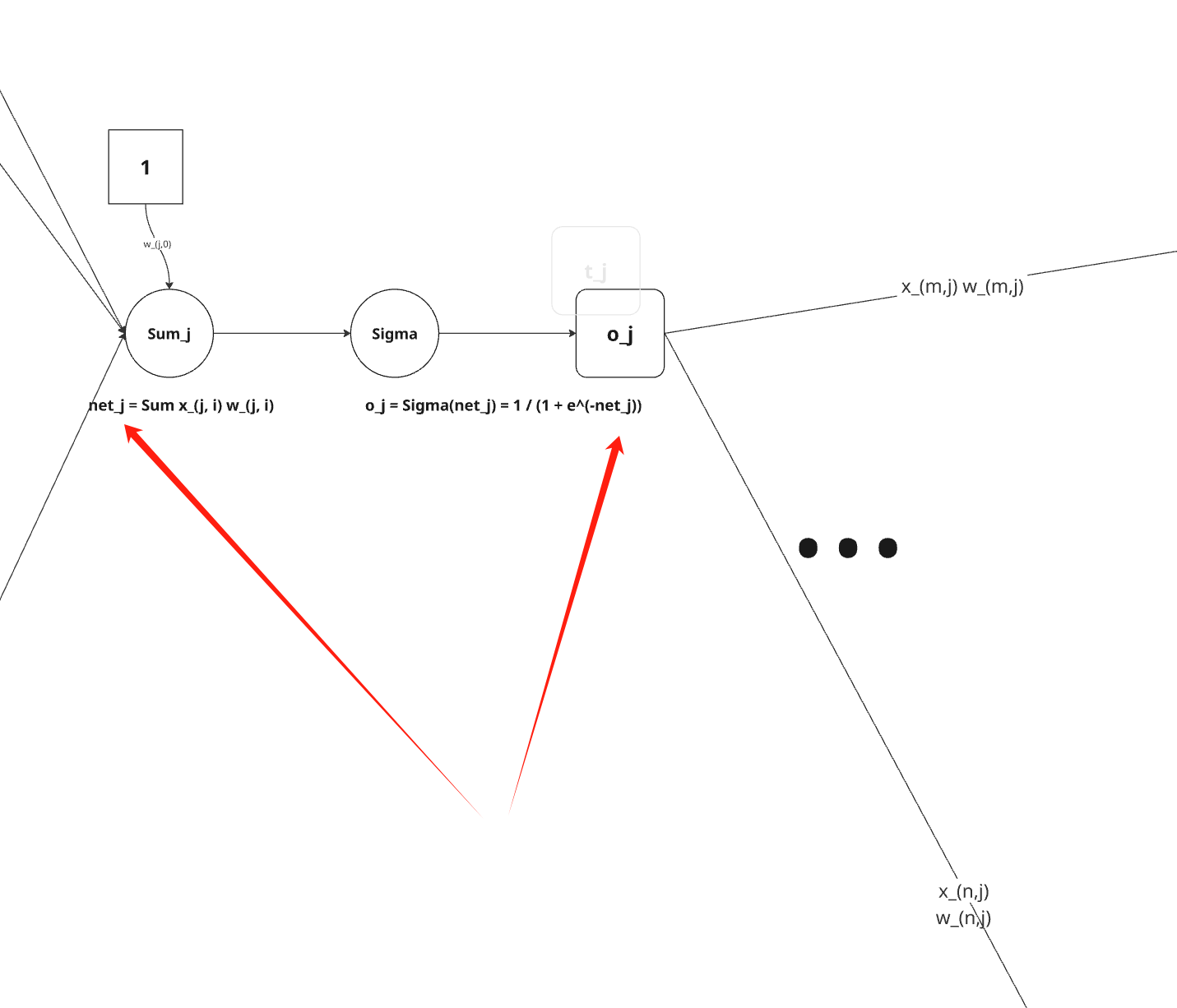
alt text

关注其中第 j 个单元，如下：

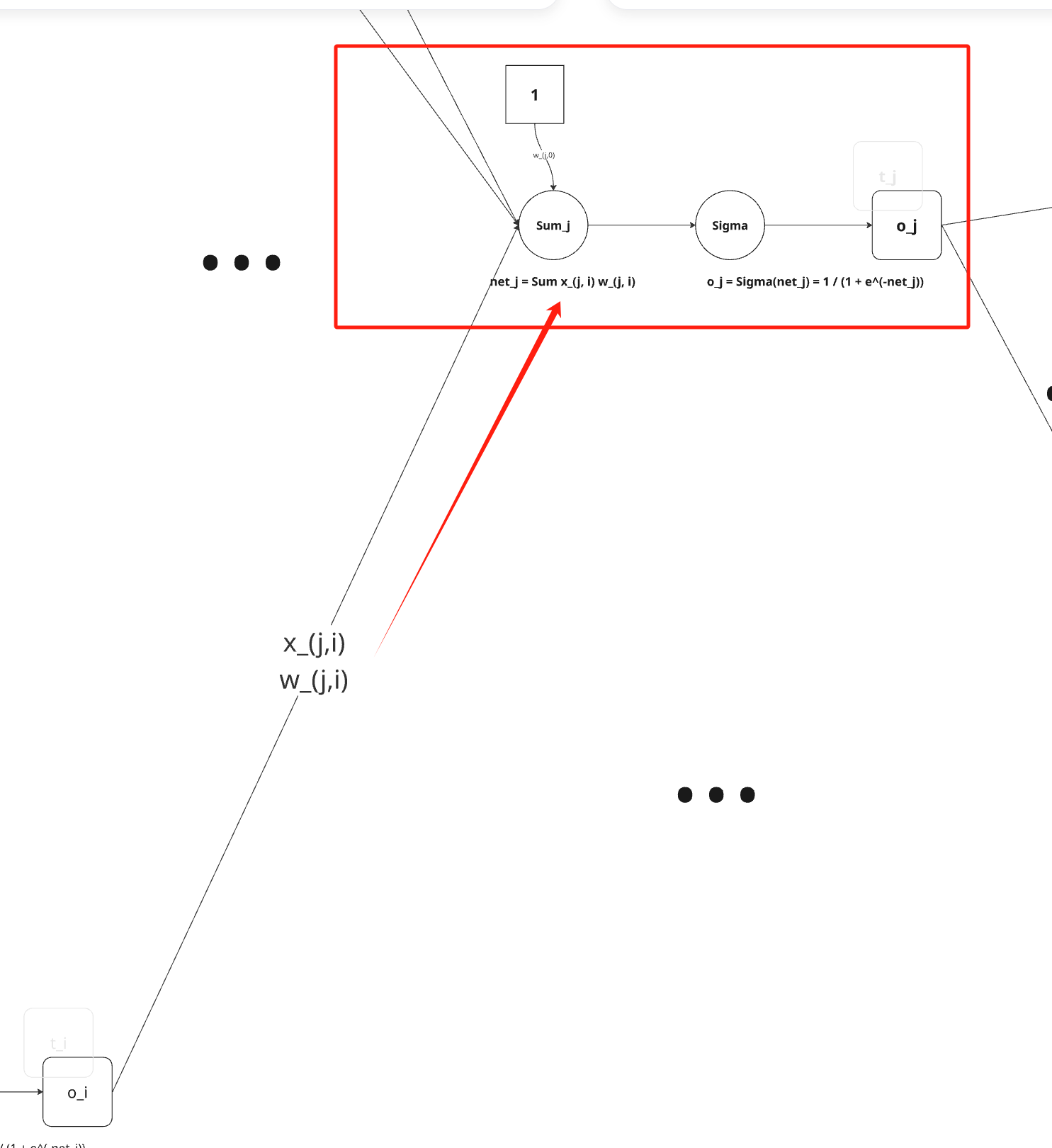
alt text

所以，我们可以使用链式法则得到：

∂Ed∂wji=∂Ed∂netj∂netj∂wji=∂Ed∂netjxji\frac{\partial E_d}{\partial w_{ji}} = \frac{\partial E_d}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}} \\ = \frac{\partial E_d}{\partial net_j} x_{ji}
(6)

于是剩下的任务就是为 ∂Ed∂netj\frac{\partial E_d}{\partial net_j} 导出一个方便的表达式。我们依次考虑两种情况：一种情况是单元j是网络中的一个输出单元，另一种情况是单元j是网络中的一个内部单元。

情况1：输出单元的权值训练法则

就像 wjiw_{ji} 仅能通过 netjnet_j 影响网络一样，netjnet_j仅能通过ojo_j影响网络。

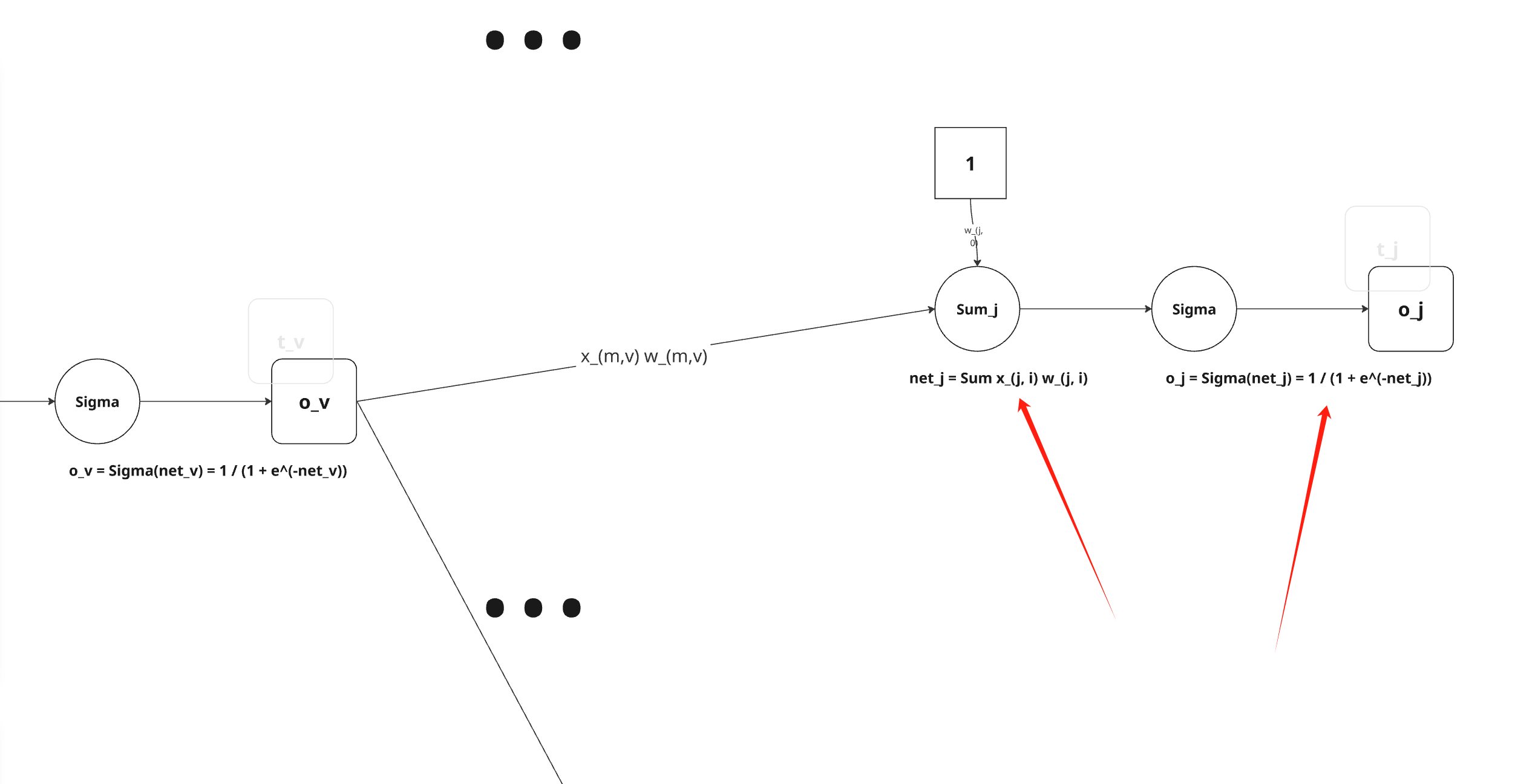
alt text

所以我们可以再次使用链式规则得出：

∂Ed∂netj=∂Ed∂oj∂oj∂netj\frac{\partial E_d}{\partial net_j} = \frac{\partial E_d}{\partial o_j} \frac{\partial o_j}{\partial net_j}
(7)

首先，仅考虑上式中的第一项：

∂Ed∂oj=∂∂oj(12∑k∈outputs(tk−ok)2)\frac{\partial E_d}{\partial o_j} = \frac{\partial}{\partial o_j}(\frac{1}{2}\sum_{k \in outputs} (t_k - o_k)^2)
(8)

除了当 k = j 时，所有输出单元 k 的导数 ∂∂oj(tk−ok)2\frac{\partial}{\partial o_j}(t_k - o_k)^2 为0。所以我们不必对多个输出单元求和，只需设 k = j。

∂Ed∂oj=∂∂oj12(tj−oj)2=122(tj−oj)∂(tj−oj)∂oj=−(tj−oj)\frac{\partial E_d}{\partial o_j} = \frac{\partial}{\partial o_j}\frac{1}{2}(t_j - o_j)^2 \\ = \frac{1}{2} 2 (t_j - o_j) \frac{\partial (t_j - o_j)}{\partial o_j} \\ = -(t_j - o_j)
(9)
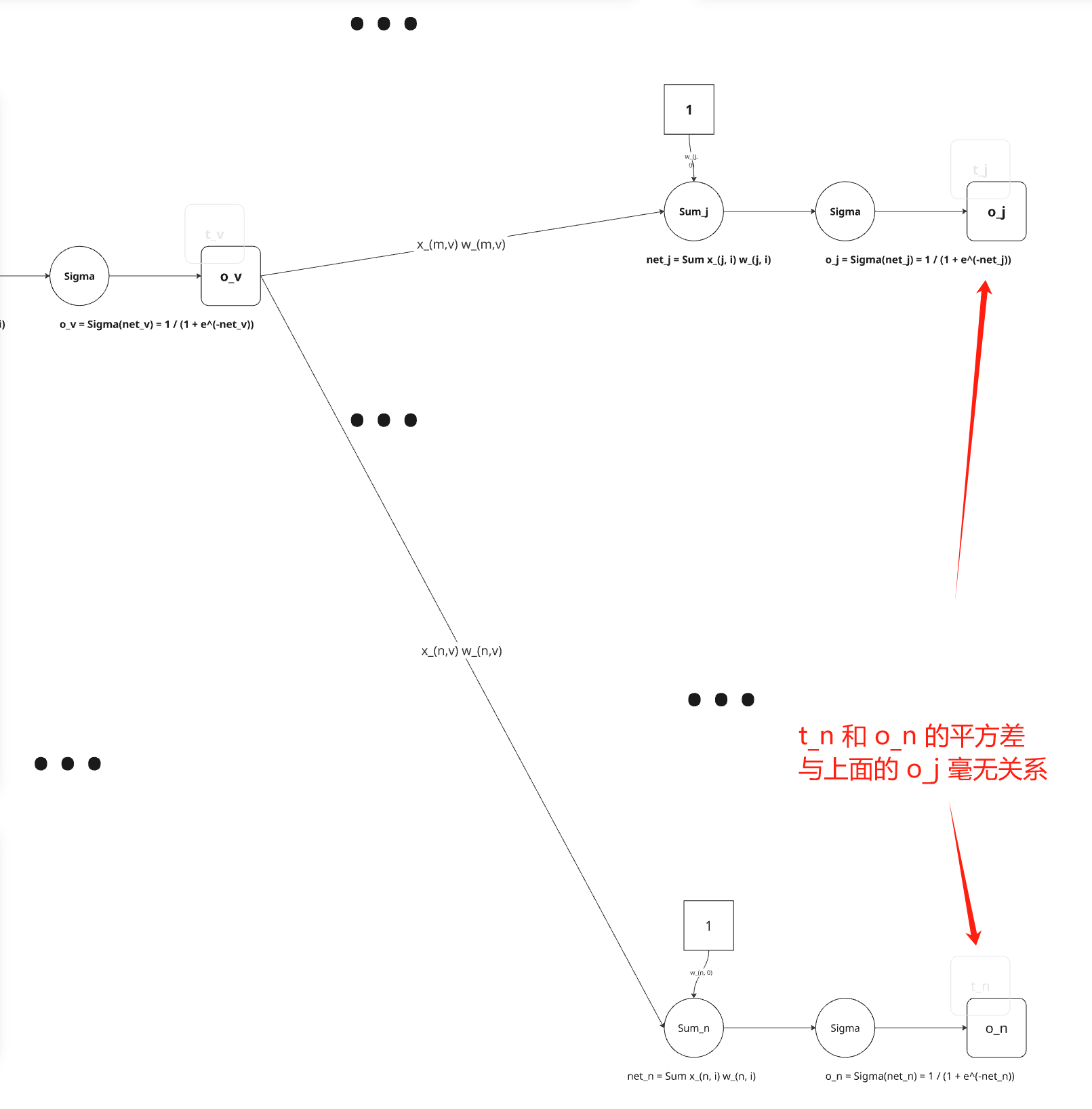
alt text

接下来考虑第二项。既然oj=σ(netj)o_j=\sigma(net_j)，导数∂oj∂netj\frac{\partial o_j}{\partial net_j} 就是 sigmoid 函数的导数，即 σ(netj)(1−σ(netj))\sigma(net_j)(1-\sigma(net_j))。所以：

∂oj∂netj=∂σ(netj)∂netj=oj(1−oj)\frac{\partial o_j}{\partial net_j} = \frac{\partial \sigma(net_j)}{\partial net_j} \\ = o_j (1 - o_j)
(10)

结合以上得到：

∂Ed∂netj=−(tj−oj)oj(1−oj)\frac{\partial E_d}{\partial net_j} = -(t_j - o_j)o_j(1-o_j)
(11)

结合以上，我们就得到了输出单元的随机梯度下降法则：

Δwji=−η∂E∂wji=−η(∑d∈D∂Ed∂wji+2γwji)=−η(∑d∈D(tj−oj)oj(1−oj)xji+2γwji)=−∑d∈Dη(tj−oj)oj(1−oj)xji−2ηγwji\Delta w_{ji} = - \eta \frac{\partial E}{\partial w_{ji}} \\ = - \eta (\sum_{d \in D} \frac{\partial E_d}{\partial w_{ji}} + 2\gamma w_{ji}) \\ = - \eta (\sum_{d \in D} (t_j - o_j) o_j (1 - o_j) x_{ji} + 2 \gamma w_{ji}) \\ = - \sum_{d \in D} \eta (t_j - o_j) o_j (1 - o_j) x_{ji} - 2 \eta \gamma w_{ji}
(12)

再回看表4-2中的权值更新法则：

wji←wji+Δwji其中Δwji=ηδjxjiw_{ji} \leftarrow w_{ji} + \Delta w_{ji} \\ 其中 \\ \Delta w_{ji} = \eta \delta_j x_{ji}
(13)

而这里，输出单元的权值更新法则就对应的是：

wji←wji−∑d∈Dη(tj−oj)oj(1−oj)xji−2ηγwjiw_{ji} \leftarrow w_{ji} - \sum_{d \in D} \eta (t_j - o_j) o_j (1 - o_j) x_{ji} - 2 \eta \gamma w_{ji}
(14)

如果令 δj=−∑d∈D(tj−oj)oj(1−oj)\delta_j = - \sum_{d \in D} (t_j - o_j) o_j (1 - o_j) ，那么输出单元的权值更新法则就是：

wji←(1−2ηγ)wji+ηδjxjiw_{ji} \leftarrow (1 - 2 \eta \gamma)w_{ji} + \eta \delta_j x_{ji}
(15)

所以，新的权值更新法则，就是在标准梯度下降权值更新以前，把每个权值乘以常数 (1−2ηγ)(1-2\eta\gamma)。

情况2：隐藏单元的权值训练法则

对于网络中的内部单元或者说隐藏单元的情况，推导 wjiw_{ji} 必须考虑 wjiw_{ji} 间接地影响网络输出，从而影响 EdE_d。由于这个原因，我们发现定义网络中单元 j 的所有直接下游单元的集合（也就是直接输入中包含单元j的输出的所有单元）是有用的。我们用 Downstream(j) 来表示这样的单元集合。

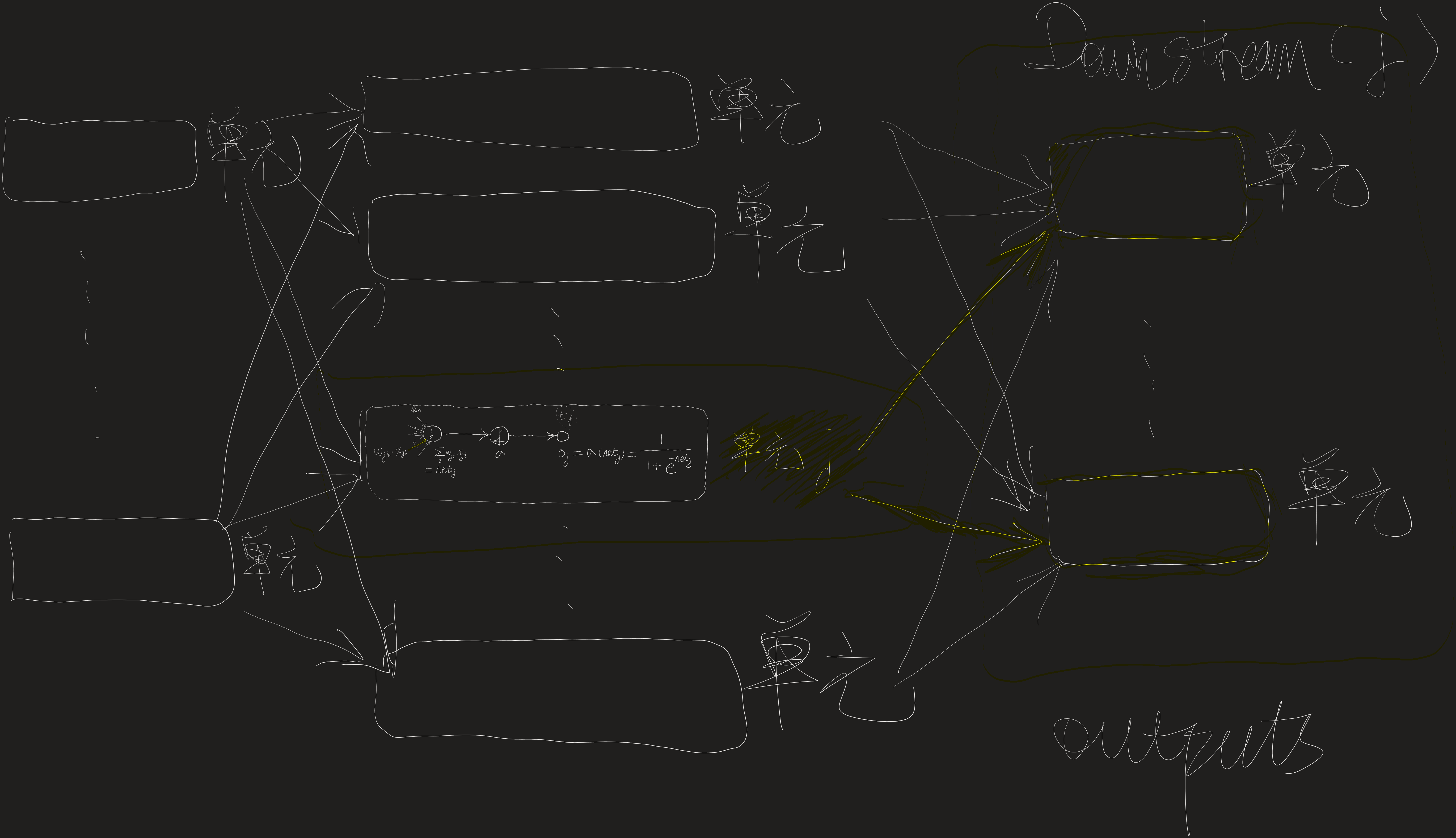
alt text

注意，netjnet_j只能通过Downstream(j)中的单元影响网络输出（再影响EdE_d）。

alt text

所以可以得出如下推导（注意，表4-2中的δk=−∂Ed∂netk\delta_k = -\frac{\partial E_d}{\partial net_k}）：

∂Ed∂netj=∑k∈Downstream(j)∂Ed∂netk∂netk∂netj=∑k∈Downstream(j)−δk∂netk∂netj=∑k∈Downstream(j)−δk∂netk∂oj∂oj∂netj=∑k∈Downstream(j)−δkwjk∂oj∂netj=∑k∈Downstream(j)−δkwjkoj(1−oj)=oj(1−oj)∑k∈Downstream(j)−δkwjk\frac{\partial E_d}{\partial net_j} = \sum_{k \in Downstream(j)} \frac{\partial E_d}{\partial net_k} \frac{\partial net_k}{\partial net_j} \\ = \sum_{k \in Downstream(j)} - \delta_k \frac{\partial net_k}{\partial net_j} \\ = \sum_{k \in Downstream(j)} - \delta_k \frac{\partial net_k}{\partial o_j} \frac{\partial o_j}{\partial net_j} \\ = \sum_{k \in Downstream(j)} - \delta_k w_{jk} \frac{\partial o_j}{\partial net_j} \\ = \sum_{k \in Downstream(j)} - \delta_k w_{jk} o_j (1-o_j) \\ = o_j (1 - o_j) \sum_{k \in Downstream(j)} - \delta_k w_{jk} \\
(16)

由于 δj=−∂Ed∂netj\delta_j = -\frac{\partial E_d}{\partial net_j}，我们可以把上式写成：

δj=oj(1−oj)∑k∈Downstream(j)δkwjk\delta_j = o_j (1 - o_j) \sum_{k \in Downstream(j)} \delta_k w_{jk} \\
(17)

于是，我们就得到了隐藏单元的随机梯度下降法则：

Δwji=−η∂E∂wji=−η(∑d∈D∂Ed∂wji+2γwji)=−η(∑d∈D∂Ed∂netj∂netj∂wji+2γwji)=−η(∑d∈D∂Ed∂netjxji+2γwji)=−η∑d∈D(−δj)xji−2ηγwji=−2ηγwji+η∑d∈Dδjxji\Delta w_{ji} = - \eta \frac{\partial E}{\partial w_{ji}} \\ = - \eta (\sum_{d \in D} \frac{\partial E_d}{\partial w_{ji}} + 2\gamma w_{ji}) \\ = - \eta (\sum_{d \in D} \frac{\partial E_d}{\partial net_j}\frac{\partial net_j}{\partial w_{ji}} + 2 \gamma w_{ji}) \\ = - \eta (\sum_{d \in D} \frac{\partial E_d}{\partial net_j} x_{ji} + 2 \gamma w_{ji}) \\ = - \eta \sum_{d \in D} (-\delta_j) x_{ji} - 2 \eta \gamma w_{ji} \\ = -2\eta \gamma w_{ji} + \eta \sum_{d \in D} \delta_j x_{ji} \\
(18)

即隐藏单元的权值更新法则是：

wji←wji+Δwjiwji←wji−2ηγwji+η∑d∈Dδjxjiwji←(1−2ηγ)wji+η∑d∈Dδjxjiw_{ji} \leftarrow w_{ji} + \Delta w_{ji} \\ w_{ji} \leftarrow w_{ji} - 2 \eta \gamma w_{ji} + \eta \sum_{d \in D} \delta_j x_{ji} \\ w_{ji} \leftarrow (1-2\eta \gamma)w_{ji} + \eta \sum_{d \in D} \delta_j x_{ji}
(19)

对比标准梯度下降权值更新法则，可以发现，对于隐藏单元来说，新的权值更新法则也是在标准梯度下降权值更新之前将每个权值乘以了常数 (1−2ηγ)(1-2\eta \gamma)。

第四章 人工神经网络
4.9
第四章 人工神经网络
4.11