Skip to article frontmatterSkip to article content

4.8

修改表 4-2 中的反向传播算法，使用双曲正切 tanh 函数取代 sigmoid 函数作为挤压函数。也就是说，假定单个单元的输出是 o=tanh(w⃗⋅x⃗) o = tanh(\vec{w} \cdot \vec{x})。给出输出层权值和隐藏层权值的权更新法则。提示：tanh′(x)=1−tanh2(x)tanh'(x) = 1 - tanh^2(x)。

修改后的表 4-2：包含两层双曲正切单元的前馈网络的反向传播算法（随机梯度下降版本）

BACKPROPAGATION(training_examples, η,nin,nout,nhidden\eta, n_{in}, n_{out}, n_{hidden})

training_examples 中每一个训练样例是形式为 <x⃗,t⃗> <\vec{x}, \vec{t}> 的序偶，其中 x⃗ \vec{x} 是网络输入值向量，t⃗\vec{t} 是目标输出值。

η 是学习速率（例如 0.05）。ninn_{in} 是网络输入的数量，nhiddenn_{hidden} 是隐藏层单元数，noutn_{out} 是输出单元数。

从单元 i 到单元 j 的输入表示为 xjix_{ji}，单元 i 到单元 j 的权值表示为 wjiw_{ji}。

其中对于误差项的计算如下：

反向传播法则的推导

这里给出反向传播算法的权值调整法则的推导。

我们要解决的问题是推导出上表算法使用的随机梯度下降法则。根据公式（11）：

Ed(w⃗)=12(td−od)2(11)E_d(\vec{w}) = \frac{1}{2} (t_d - o_d)^2 \tag{11}
(10)

，随机的梯度下降算法迭代处理训练样例，每次处理一个。对于每个训练样例 d，利用关于这个样例的误差

EdE_d
(11)

的梯度修改权值。换句话说，对于每一个训练样例d，每个权

wjiw_{ji}
(12)

被增加

Δwji\Delta w_ji
(13)

：

Δwji=−η∂Ed∂wji(12)\Delta w_{ji} = -\eta\frac{\partial E_d}{\partial w_{ji}} \tag{12}
(14)

其中，

EdE_d
(15)

是训练样例d的误差，通过对网络中所有输出单元的求和得到：

Ed(w⃗)≡12∑k∈outputs(tk−ok)2E_d({\vec{w}}) \equiv \frac{1}{2} \sum_{k \in outputs}(t_k - o_k)^2
(16)

这里，outputs 是网络中输出单元的集合，

tkt_k
(17)

是单元k对于训练样例d的目标值，

oko_k
(18)

是给定训练样例d时单元k的输出值。

随机梯度下降法则的推导在概念上是易懂的，但需要留意很多下标和变量。我们将遵循下图中所画出的符号，增加一个下标 j 用来表示网络中第 j 个单元。

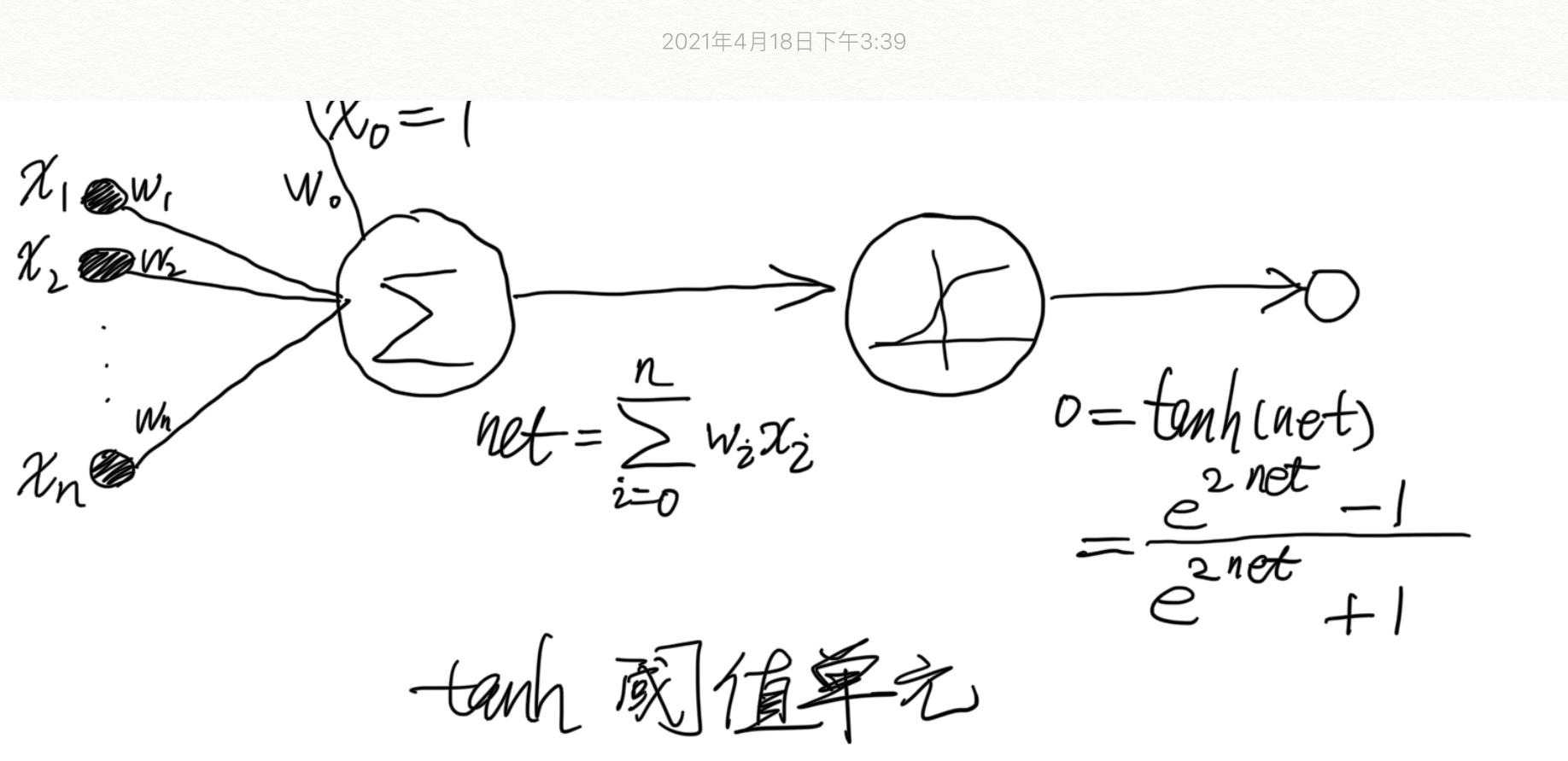
tanh 阈值单元

具体如下：

现在我们导出

∂Ed∂wji\frac{\partial E_d}{\partial w_{ji}}
(27)

的一个表达式，以便实现公式（12）中所讲的随机梯度下降法则。首先，注意权值

wjiw_{ji}
(28)

仅能通过

netjnet_j
(29)

影响网络的其他部分。所以，我们可以使用链式规则得到：

∂Ed∂wji=∂Ed∂netj∂netj∂wji\frac{\partial E_d}{\partial w_{ji}} = \frac{\partial E_d}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}}
(30)
=∂Ed∂netjxji(13)= \frac{\partial E_d}{\partial net_j} x_{ji} \tag{13}
(31)

已知等式（13），我们剩下的任务就是为

∂Ed∂netj\frac{\partial E_d}{\partial net_j}
(32)

导出一个方便的表达式。我们依次考虑两种情况：一种情况是单元 j 是网络中的一个输出单元，另一种情况是 j 是一个内部单元。

情况 1：输出单元的权值训练法则

就像

wjiw_{ji}
(33)

仅能通过

netjnet_j
(34)

影响网络一样，

netjnet_j
(35)

仅能通过

ojo_j
(36)

影响网络。所以我们可以再次使用链式规则得出：

∂Ed∂netj=∂Ed∂oj∂oj∂netj(14)\frac{\partial E_d}{\partial net_j} = \frac{\partial E_d}{\partial o_j} \frac {\partial o_j}{\partial net_j} \tag{14}
(37)

首先，仅考虑上式（14）中的第一项：

∂Ed∂oj=∂∂oj12∑k∈outputs(tk−ok)2\frac{\partial E_d}{\partial o_j} = \frac{\partial}{\partial o_j} \frac{1}{2} \sum_{k \in outputs} (t_k - o_k)^2
(38)

除了当k=j时，所有输出单元k的导数

∂∂oj(tk−ok)2\frac{\partial}{\partial o_j}(t_k - o_k)^2
(39)

为0.所以我们不必对多个输出单元求和，只需要设k = j。

∂Ed∂oj=∂∂oj12(tj−oj)2\frac{\partial E_d}{\partial o_j} = \frac{\partial }{\partial o_j}\frac{1}{2}(t_j - o_j)^2
(40)
=122(tj−oj)∂(tj−oj)∂oj=\frac{1}{2} 2 (t_j - o_j) \frac{\partial (t_j - o_j)}{\partial o_j}
(41)
=−(tj−oj)(15)=-(t_j-o_j) \tag{15}
(42)

接下来考虑公式（14）中的第二项。既然

oj=tanh⁡(netj)o_j = \tanh(net_j)
(43)

，导数

∂oj∂netj\frac{\partial o_j}{\partial net_j}
(44)

就是

tanh⁡\tanh
(45)

函数的导数，由提示可知：

tanh⁡′(netj)=1−tanh⁡2(netj)\tanh'(net_j) = 1 - \tanh^2(net_j)
(46)

。所以：

∂oj∂netj=∂tanh⁡(netj)∂netj\frac{\partial o_j}{\partial net_j} = \frac{\partial \tanh(net_j)}{\partial net_j}
(47)
=1−oj2(16)= 1 - o^2_j \tag{16}
(48)

把表达式（15）和（16）代入（14），我们得到：

∂Ed∂netj=−(tj−oj)(1−oj2)(17)\frac{\partial E_d}{\partial net_j} = -(t_j - o_j)(1- o^2_j) \tag{17}
(49)

然后与公式（12）和（13）合并，我们便推导出了输出单元的随机梯度下降法则：

Δwji=−η∂Ed∂wji=η(tj−oj)(1−oj2)xji(18)\Delta w_{ji} = -\eta \frac{\partial E_d}{\partial w_{ji}} = \eta (t_j - o_j)(1-o^2_j)x_{ji} \tag{18}
(50)

注意，这个训练法则恰恰是修改后的表4-2算法中的公式（4.14）和公式（4.16）的权值更新法则。此外，我们可以发现公式（4.14）中的

δk\delta_k
(51)

与

−∂Ed∂netk-\frac{\partial E_d}{\partial net_k}
(52)

的值相等，所以可以使用

δi\delta_i
(53)

来表示任意单元i的

−∂Ed∂netj-\frac{\partial E_d}{\partial net_j}
(54)

。

情况 2：隐藏单元的权值训练法则

对于网络中的内部单元或者说隐藏单元的情况，推导

wjiw_{ji}
(55)

必须考虑

wjiw_{ji}
(56)

间接地影响网络输出，从而影响

EdE_d
(57)

。由于这个原因，我们发现定义网络中单元j地所有直接下游单元的集合（也就是直接输入中包含单元 j 的输出的所有单元）是有用的。我们用 Downstream(j) 表示这样的单元集合。注意，

netjnet_j
(58)

只能通过Downstream(j)中的单元影响网络输出（再影响

EdE_d
(59)

）。所以可以得出如下推导：

∂Ed∂netj=∑k∈Downstream(j)∂Ed∂netk∂netk∂netj\frac{\partial E_d}{\partial net_j} = \sum_{k \in Downstream(j)} \frac{\partial E_d}{\partial net_k} \frac{\partial net_k}{\partial net_j}
(60)
=∑k∈Downstream(j)−δk∂netk∂netj= \sum_{k \in Downstream(j)} - \delta_k \frac{\partial net_k}{\partial net_j}
(61)
=∑k∈Downstream(j)−δk∂netk∂oj∂oj∂netj= \sum_{k \in Downstream(j)} - \delta_k \frac{\partial net_k}{\partial o_j} \frac{\partial o_j}{\partial net_j}
(62)
=∑k∈Downstream(j)−δkwkj∂oj∂netj= \sum_{k \in Downstream(j)} - \delta_k w_{kj} \frac{\partial o_j}{\partial net_j}
(63)
=∑k∈Downstream(j)−δkwkj(1−oj2)= \sum_{k \in Downstream(j)} - \delta_k w_{kj} (1-o^2_j)
(64)

重新组织各项并使用

δj\delta_j
(65)

表示

−∂Ed∂netj-\frac{\partial E_d}{\partial net_j}
(66)

，我们得到：

δj=(1−oj2)∑k∈Downstream(j)δkwkj\delta_j = (1-o^2_j) \sum_{k \in Downstream(j)}\delta_k w_{kj}
(67)

和

Δwji=ηδjxji\Delta w_{ji} = \eta \delta_j x_{ji}
(68)

上式就是由公式（4.19）得到的一般法则，用来更新任意有向无环网络结构内部单元的权值。

δr=(1−or2)∑s∈Downstream(r)wsrδs(4.19)\delta_r = (1-o^2_r) \sum_{s \in Downstream(r)} w_{sr} \delta_s \tag{4.19}
(69)

注意，修改后表4-2中的公式（4.15）仅是这个法则当Downstream(j) = outputs时的一个特例。

第四章 人工神经网络
4.7
第四章 人工神经网络
X1x8.network